Prof. Mauro
ESERCIZI SULLE DERIVATE
1)
Calcolare, nel punto di ascissa ![]() , la derivata della funzione
, la derivata della funzione ![]() ,
servendosi della sola definizione di derivata.
,
servendosi della sola definizione di derivata.
Si ricorda la definizione di derivata in un punto:
La derivata della funzione ![]() nel suo
punto di ascissa
nel suo
punto di ascissa ![]() è
il limite, se esiste ed è finito, del rapporto incrementale della
funzione al tendere a zero dell’incremento h della variabile,
è
il limite, se esiste ed è finito, del rapporto incrementale della
funzione al tendere a zero dell’incremento h della variabile,
ossia :
![]() .
.
Pertanto, si ha:
![]()
![]()
![]()
Quindi, sostituendo nel limite, si ottiene:
![]() .
.
2)
Calcolare, nel punto di ascissa ![]() , la derivata della funzione
, la derivata della funzione ![]() ,
servendosi della sola definizione di derivata.
,
servendosi della sola definizione di derivata.
Pertanto, si ha:
![]()
![]()
![]()
Quindi, per la definizione di derivata in un punto, si ottiene:
![]()
3)
Calcolare, nel punto di ascissa ![]() , la derivata della funzione
, la derivata della funzione ![]() ,
servendosi della sola definizione di derivata. Interpretare geometricamente
l’esercizio.
,
servendosi della sola definizione di derivata. Interpretare geometricamente
l’esercizio.
Pertanto, si ha:
![]()
![]()
![]()
Quindi, per la definizione di derivata in un punto, si ottiene:
![]()
Il valore 2 è il
coefficiente angolare della retta tangente alla parabola di equazione ![]() nel punto
di tangenza
nel punto
di tangenza ![]() .
.
1° metodo:
Per trovare l’equazione della retta tangente nel punto di tangenza si può applicare la regola dello sdoppiamento all’equazione della curva, cioè:
![]()
dove ![]() e
e ![]() sono le coordinate del punto di tangenza, pertanto,
sostituendo si ottiene:
sono le coordinate del punto di tangenza, pertanto,
sostituendo si ottiene:
![]() ,
,
ossia:
![]() ,
,
che è l’equazione della retta tangente, avente come coefficiente angolare il valore 2.
2° metodo:
Oppure, si perviene alla stessa conclusione, utilizzando la formula per trovare l’equazione della retta, conoscendo le coordinate del punto di tangenza e il coefficiente angolare, cioè:
![]() ,
,
ossia:
![]() .
.
Sostituendo ![]() ,
, ![]() e
e ![]() , si ottiene:
, si ottiene:
![]()
cioè:
![]() .
.
Graficamente si ha:
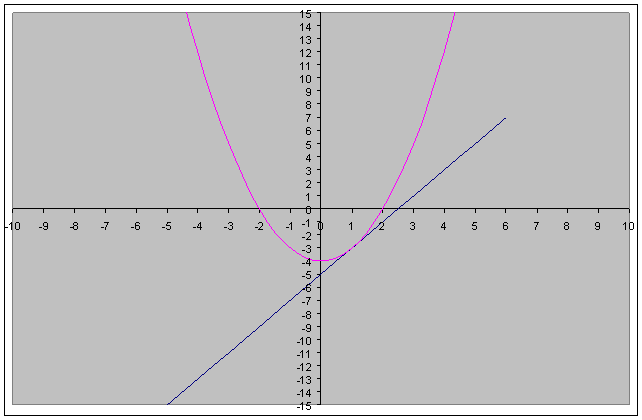
(Vedi anche relativo programma in Excel)
4)
Calcolare, nel punto di ascissa ![]() , la derivata della funzione
, la derivata della funzione ![]() ,
servendosi della sola definizione di derivata. Interpretare geometricamente
l’esercizio.
,
servendosi della sola definizione di derivata. Interpretare geometricamente
l’esercizio.
Pertanto, si ha:
![]()
![]()
![]() ,
,
ossia:
![]()
Quindi, per la definizione di derivata in un punto, si ottiene:
![]()
Il valore 3 è il
coefficiente angolare della retta tangente alla cubica di equazione ![]() nel punto di tangenza
nel punto di tangenza ![]() .
.
La formula per trovare l’equazione della retta, conoscendo le coordinate del punto di tangenza e il coefficiente angolare, è:
![]() ,
,
ossia:
![]() .
.
Sapendo che ![]() ,
, ![]() e
e ![]() , si ottiene:
, si ottiene:
![]()
cioè:
![]() .
.
Graficamente si ha:
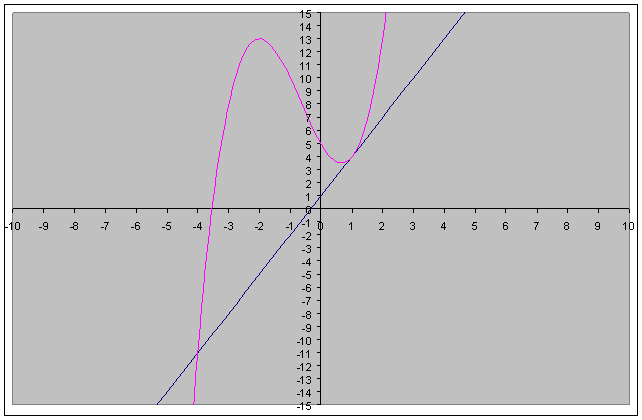
(vedi anche relativo programma in Excel)