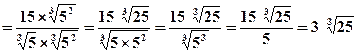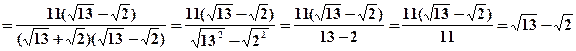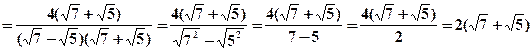Prof. Mauro La Barbera

Home page

Classe seconda

Radicali

Esercizi svolti

1) Calcolare la seguente somma algebrica di radicali:

Si possono sommare i radicali simili, cioè quando hanno lo stesso indice e lo stesso radicando, pertanto, sommando algebricamente i coefficienti dei radicali simili, si ottiene:

2) Ridurre allo stesso indice i seguenti radicali:

; .

Si trova il minimo comune multiplo degli indici, cioè 6 , si divide questo numero per l’indice 2 del primo radicale e si moltiplica il risultato 3 per l’esponente del radicando , che diventa , analogamente si procede per il secondo radicale, pertanto si ha:

; .

3) Moltiplicare i seguenti radicali:

Il prodotto di due radicali aventi lo stesso indice è un radicale del medesimo indice, avente per radicando il prodotto dei radicandi, cioè si ottiene:

In questo caso poiché i radicali non hanno lo stesso indice, prima è necessario ridurli allo stesso indice e poi eseguire la moltiplicazione, cioè:

4) Dividere i seguenti radicali:

Il quoziente di due radicali aventi lo stesso indice è un radicale del medesimo indice, avente per radicando il quoziente dei radicandi, cioè si ottiene:

In questo caso poiché i radicali non hanno lo stesso indice, prima è necessario ridurli allo stesso indice e poi eseguire la divisione, cioè:

5) Semplificare i seguenti radicali:

Il radicale per definizione è una potenza ad esponente frazionario, quindi la base ha per esponente una frazione, il cui numeratore è l’esponente 8, mentre il denominatore è l’indice 2 della radice, analogamente si ha per la base , la quale ha ad esponente la frazione pertanto, il radicale dato si può scrivere nel seguente modo:

semplificando le frazioni, si ottiene

=

=

=

6) Portare i possibili fattori fuori dal segno di radice dei seguenti radicali:

Si esegue la divisione tra gli esponenti dei fattori che formano il radicando e l’indice della radice, pertanto per il fattore si ottiene:

il quoziente 1 indica quanti fattori a escono fuori dal segno di radice, mentre il resto 2 indica quanti fattori rimangono dentro il segno di radice, per il fattore , si ottiene:

il quoziente 2 indica quanti fattori escono fuori dal segno di radice, mentre il resto 1 indica che rimane una sola dentro il segno di radice, cioè:

7) Portare i fattori dentro il segno di radice dei seguenti radicali:

Si moltiplica l’esponente 3 del fattore per l’indice 2 della radice e il prodotto lo si addiziona all’esponente del radicando, cioè:

8) Razionalizzare i denominatori dei seguenti radicali:

Si moltiplica sia il numeratore che il denominatore della frazione per , pertanto, si ottiene:

9) Razionalizzare il denominatore del seguente radicale:

Si osserva che l’indice della radice è 3 , mentre l’esponente del radicando è 1 , quindi si moltiplica sia il numeratore che il denominatore della frazione per (l’esponente 2 della base 5 è dato dalla sottrazione tra 3 e 1), pertanto, si ottiene:

10) Razionalizzare il denominatore dato dalla somma di due radicali:

Per razionalizzare il denominatore bisogna applicare la seguente regola dei prodotti notevoli “La somma di due monomi per la loro differenza è uguale alla differenza dei quadrati dei monomi”, cioè . Quindi moltiplicando sia il denominatore che il numeratore per il complementare si ottiene:

11) Razionalizzare il denominatore dato dalla differenza di due radicali:

Per razionalizzare il denominatore bisogna applicare la seguente regola dei prodotti notevoli “La somma di due monomi per la loro differenza è uguale alla differenza dei quadrati dei monomi”, cioè . Quindi moltiplicando sia il denominatore che il numeratore per il complementare si ottiene: