Prof. Mauro La Barbera

Home page

Classe quinta

ANALISI MATEMATICA

ESERCIZIO SVOLTO

Determinare il dominio della funzione

La funzione data è algebrica irrazionale intera di secondo grado (semicirconferenza), scritta in forma esplicita, per determinare il campo di esistenza si pone il radicando maggiore o uguale a zero (si osserva che la radice è di indice pari), cioè

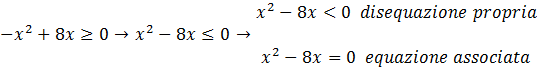
Per risolvere la disequazione suddetta si passa inizialmente alla risoluzione della sua equazione “interna” associata, ossia

Ricordando che e si ha

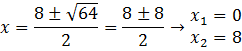
Per calcolare le soluzioni della disequazione si può applicare il metodo della risoluzione grafica, pertanto, ponendo si ha un’equazione bidimensionale, che nel piano cartesiano è rappresentata da una parabola. La curva interseca l’asse delle ascisse nei punti , e ha il vertice nel punto . La disequazione è verificata per tutti i punti del grafico della parabola situati al di sotto dell’asse delle ascisse (per tutti i valori delle ascisse che hanno immagini negative), cioè, ossia per tutti i valori interni all’intervallo delle soluzioni dell’equazione associata.

Pertanto, la disequazione è verificata per 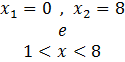cioè per .

Quindi, il dominio della funzione data è .

Infatti costruendo il grafico della funzione si osserva che il disegno si estende per

Metodo algebrico

Il binomio che si trova al primo membro della disequazione si può scomporre nel seguente modo

Il prodotto è positivo quando i due fattori hanno lo stesso segno (concordi), pertanto, ponendo che entrambi siano positivi, si ha

Schematizzando sull’asse delle ascisse si ottiene

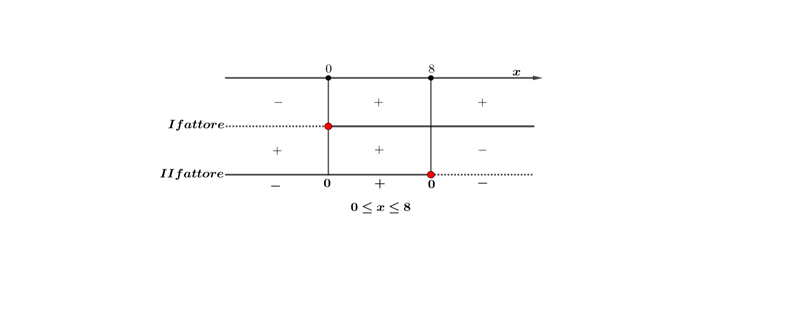
Regola algebrica

<	>
>	>