Omotetia Home page

Prof. Mauro La Barbera

“Omotetia nel piano cartesiano”

Competenze:

Ø Usare le tecniche e le procedure di calcolo aritmetico ed algebrico.

Ø Utilizzare il linguaggio e i metodi propri della matematica per organizzare e valutare adeguatamente informazioni qualitative e quantitative

Abilità:

v Saper applicare la condizione di parallelismo e perpendicolarità tra le rette del piano.

v Saper determinare le equazioni dell’omotetia.

v Saper calcolare le misure delle figure nel piano cartesiano.

v Saper costruire figure nel piano cartesiano.

Nel piano cartesiano Oxy disegnare il triangolo avente per vertici i punti , e . Determinare:

a) il perimetro del triangolo ABC;

b) l’area del triangolo ABC;

Dopo aver disegnare il triangolo A’B’C’ trasformato dall’omotetia di centro l’origine degli assi cartesiani e di rapporto applicata al triangolo ABC, determinare:

c) il perimetro del triangolo A’B’C’;

d) l’area del triangolo A’B’C’;

Svolgimento

Dalla figura si osserva che il triangolo dato è un triangolo rettangolo isoscele. Per determinare la misura del lato AB del triangolo ABC si applica la seguente formula:

Per determinare la misura del lato BC del triangolo ABC si applica la seguente formula:

Per determinare la misura del lato AC del triangolo ABC si applica la seguente formula:

.

Il perimetro del triangolo è cioè .

L’area del triangolo è ossia

Per disegnare il triangolo A’B’C’ trasformato dall’omotetia di centro l’origine degli assi cartesiani e di rapporto applicata al triangolo ABC, si utilizzano le seguenti equazioni:

Pertanto il triangolo A’B’C’ omotetico al triangolo ABC ha per vertici i seguenti punti omotetici , e .

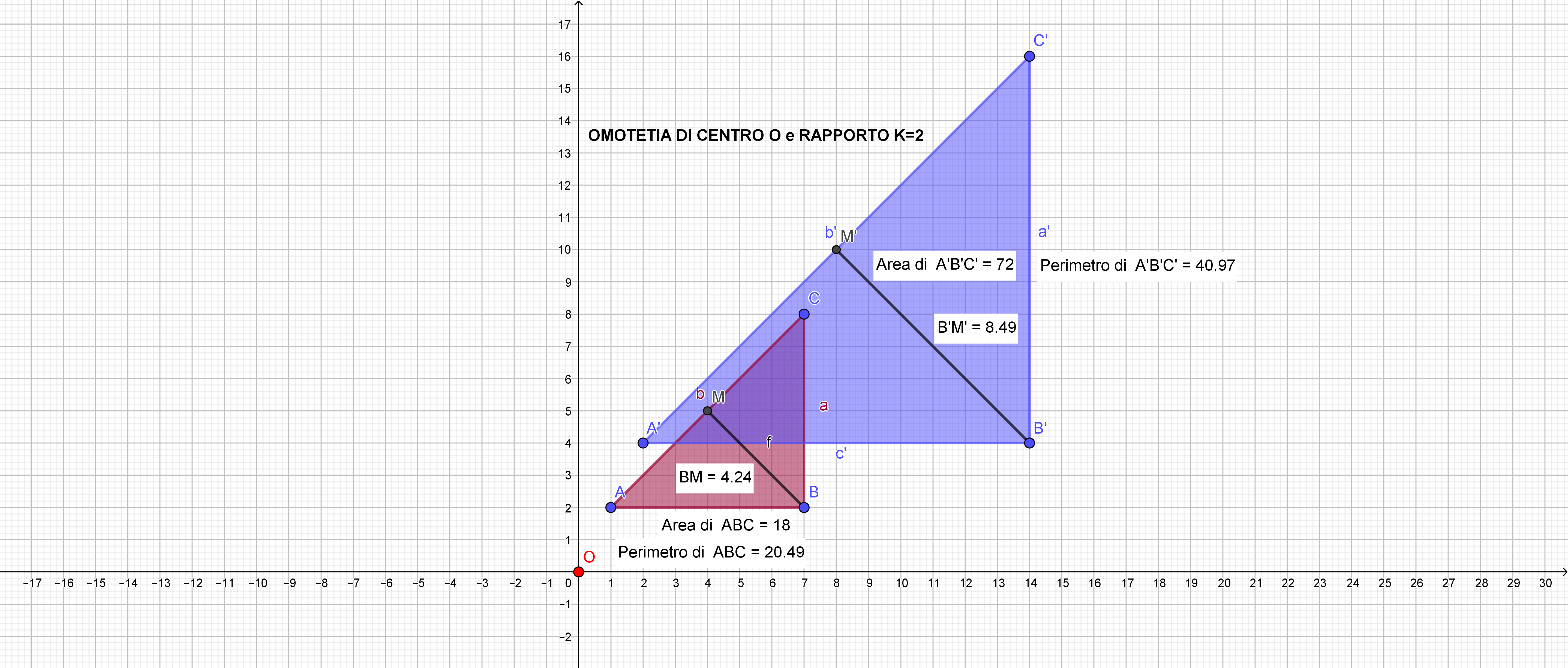
Gli elementi omotetici richiesti sono:

.

.

Osservazione:

Per determinare l’area di un triangolo conoscendo le coordinate dei suoi vertici si può applicare la seguente formula:

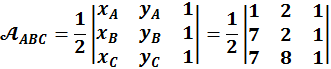
Sviluppando il determinante si ha

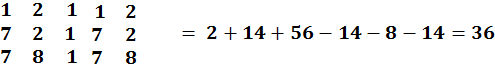
Pertanto .