Prof. Mauro La Barbera
Un
problema di geometria risolto con un’equazione di primo grado
In un rettangolo la base supera di tre metri il triplo
dell’altezza e il perimetro è di metri 62. Determinare l’area della figura.
Ponendo 
si deduce che 
.
Pertanto, sapendo che il perimetro è 
ha senso
scrivere:
Sostituendo si ottiene:
Ossia:
Cioè:
Quindi l’altezza 
metri, mentre
la base 
metri.
L’area del rettangolo è 
metri al
quadrato.
Un
problema di geometria risolto con un’equazione di secondo grado
In un rettangolo il perimetro misura 22
metri, mentre l’area misura 24 metri al quadrato. Determinare le dimensioni
della figura sapendo che la base è maggiore dell’altezza.
Sapendo che il perimetro è 
ha senso
scrivere:
Inoltre, l’area è
Pertanto, si conosce sia la somma che il prodotto di
due numeri, quindi si può scrivere la seguente equazione di secondo grado:
dove S
e P indicano, rispettivamente, la
somma e il prodotto dei due numeri, allora sostituendo i dati si ha:
Cioè:
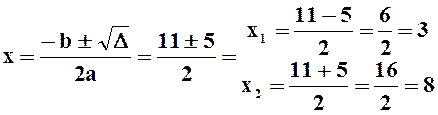
Si ottiene che l’altezza 
metri, mentre
la base 
metri.