Prof. Mauro La Barbera

Home page

Classe terza

Geometria analitica

SIMMETRIA RISPETTO ALL’ASSE DELLE ORDINATE

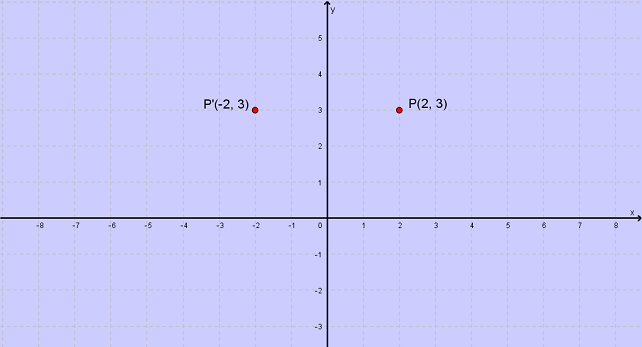
In un sistema di assi cartesiani ortogonali Oxy dato un punto P di coordinate (x;y) , si definisce simmetrico di P rispetto all’asse delle ordinate e si indica con P’ il punto che ha la stessa ordinata, ma ascissa opposta, cioè P’ (-x;y) . L'asse delle y è l'asse del segmento PP', pertanto, questa trasformazione geometrica dei punti del piano è una simmetria assiale, ed è un caso particolare di isometria, cioè conserva la lunghezza dei segmenti, ossia è una trasformazione che non modifica le distanze tra i punti.  Esempio:

SIMMETRIA RISPETTO ALL’ASSE DELLE ASCISSE

In un sistema di assi cartesiani ortogonali Oxy dato un punto P di coordinate (x;y) , si definisce simmetrico di P rispetto all’asse delle ascisse e si indica con P’ il punto che ha la stessa ascissa, ma ordinata opposta, cioè P’ (x;-y) . L'asse delle x è l'asse del segmento PP', pertanto, questa trasformazione geometrica dei punti del piano è una simmetria assiale, ed è un caso particolare di isometria, cioè conserva la lunghezza dei segmenti, ossia è una trasformazione che non modifica le distanze tra i punti. Esempio:

SIMMETRIA RISPETTO ALL’ORIGINE DEGLI ASSI CARTESIANI

In un sistema di assi cartesiani ortogonali Oxy dato un punto P di coordinate (x;y) , si definisce simmetrico di P rispetto all’origine degli assi cartesiani e si indica con P’ il punto che ha ascissa ed ordinata opposte, cioè P’ (-x;-y) . Questa trasformazione geometrica dei punti del piano è una simmetria centrale, l'origine degli assi cartesiani è il centro di simmetria, ossia è il punto medio del segmento PP'.  Esempio:

SIMMETRIA RISPETTO ALLA BISETTRICE DEL I E III QUADRANTE

In un sistema di assi cartesiani ortogonali Oxy dato un punto P di coordinate (x;y) , si definisce simmetrico di P rispetto alla bisettrice del primo e terzo quadrante e si indica con P’ il punto che ha le coordinate permutate, cioè P’ (y;x) . Esempio:

SIMMETRIA RISPETTO ALLA BISETTRICE DEL II E IV QUADRANTE

In un sistema di assi cartesiani ortogonali Oxy dato un punto P di coordinate (x;y) , si definisce simmetrico di P rispetto alla bisettrice del secondo e quarto quadrante e si indica con P’ il punto che ha le coordinate permutate ed opposte, cioè P’ (-y;-x) . Esempio:

SIMMETRIA CENTRALE RISPETTO AL CENTRO C

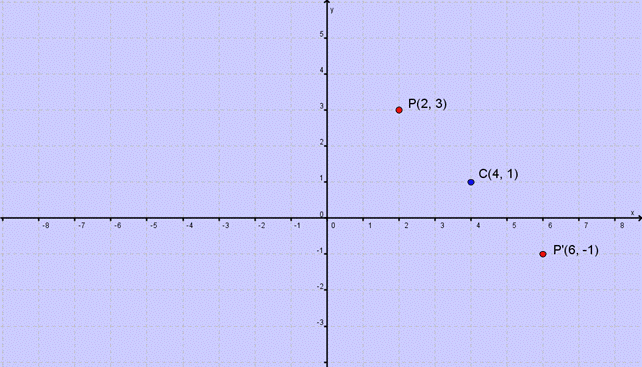
In un sistema di assi cartesiani ortogonali Oxy dato un punto P di coordinate (x;y) , si definisce simmetrico di P rispetto al punto C(x_c ; y_c) , centro di simmetria, e si indica con P’ il punto che verifica le seguenti condizioni .  Il punto C è il punto medio del segmento PP'. Esempio:

FORMULARIO

Rispetto all’asse delle ordinate

Rispetto all’asse delle ascisse

Rispetto all’origine degli assi

Rispetto alla bisettrice del I e III quadrante

Rispetto alla bisettrice del II e IV quadrante

Rispetto al centro C

Torna su