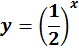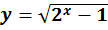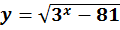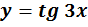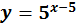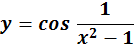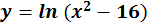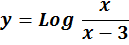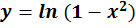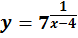DOMINIO DI UNA FUNZIONE n°4
Prof. Mauro La Barbera
Determinare il campo di esistenza delle seguenti funzioni trascendenti:
- ]-∞ ; +∞[
- [-∞ ; +∞]
- [-2 ; 2]
- ]-1 ; 1[
- [0 ; +∞[
- ]-∞ ; 0[ U ]0 ; +∞[
- ]1 ; +∞[
- ]-∞ ; +∞[
- ]3 ; +∞[
- ]-∞ ; +∞[
- ]-∞ ; -81[ U ]-81 ; +∞[
- [4 ; +∞[
- Per tutti i valori di x tranne per x = π/3 + 2kπ
- Per tutti i valori di x tranne per x = π/6 + kπ/2
- Per tutti i valori di x tranne per x = π/2 + kπ
- Per tutti i valori di x tranne per x = π/6 + kπ/3
- ]-∞ ; 5[ U ]5 ; +∞[
- ]-5 ; +5[
- ]-∞ ; +∞[
- ]-∞ ; -5[ U ]-5 ; +∞[
- ]-∞ ; -1[ U ]1 ; +∞[
- ]-1 ; +1[
- ]-∞ ; +∞[
- ]-∞ ; -1[ U ]-1 ; 1[ U ]1 ; +∞[
- ]16 ; +∞[
- ]-∞ ; -4[ U ]4 ; +∞[
- ]-∞ ; -4[ U ]-4 ; 4[ U ]4 ; +∞[
- [-4 ; 4]
- ]-∞ ; -3[ U ]3 ; +∞[
- ]-∞ ; +∞[
- ]-∞ ; 0[ U ]3 ; +∞[
- ]-∞ ; 0[ U ]0 ; 3[ U ]3 ; +∞[
- [-1 ; +∞]
- ]-∞ ; +∞[
- ]-1 ; +1[
- [-1 ; +∞[
- ]-∞ ; 4[ U ]4 ; +∞[
- ]0 ; +∞[
- ]-∞ ; 0[
- [-4 ; +4[