Prof. Mauro
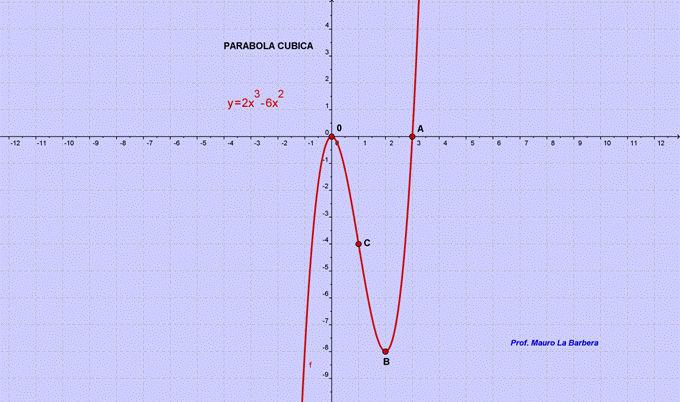
STUDIO DELLA FUNZIONE CUBICA
1) Classificazione e Campo di esistenza
Funzione algebrica razionale intera di
terzo grado, parabola cubica, la sua forma implicita è 
.
C. E.:
(simbologia insiemistica) o 
(simbologia topologica).
2) Simmetrie
Si
pone 
allora 
ossia 
, quindi la funzione non è simmetrica sia
rispetto all’asse delle ordinate (pari) che rispetto all’origine degli assi
cartesiani (dispari), perché: 
.
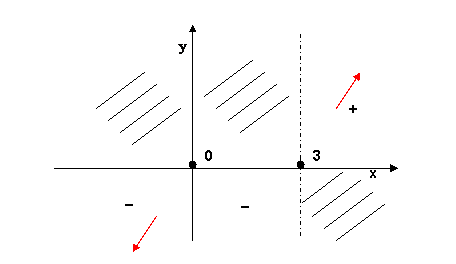
3) Studio del segno
Si pone il secondo membro dell’equazione
della funzione maggiore o uguale a zero, cioè:
cioè: 
, pertanto, si può
scrivere:
1 fattore: 
(la disequazione è
sempre verificata),
2 fattore: 
cioè 
quindi per 
.
Quindi,
per 
la funzione è
positiva, mentre per 
e per 
la funzione è
negativa. Infine, per 
e per 
la funzione è nulla.
4) Intersezioni con gli assi
cartesiani
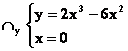ossia passa per l’origine degli assi cartesiani.
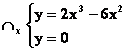interseca l’asse delle x, oltre nel punto 
, anche nel punto 
.
5) Andamento della funzione agli estremi dell’intervallo del dominio
Poiché
l’intervallo di esistenza della funzione è , si calcolano i limiti della funzione negli estremi
dell’intervallo del campo di esistenza. Pertanto, per 
si ha 
. Il
limite dà una forma indeterminata, per eliminare la forma di indecisione si
mette in evidenza la 
di grado massimo, cioè
, mentre per 
si ottiene che 
6) Crescenza e/o decrescenza
Si
calcola la derivata prima della funzione, cioè: 
, si pone poi la derivata
prima maggiore o uguale a zero, cioè: 
, ossia: 
, pertanto, si ottiene:
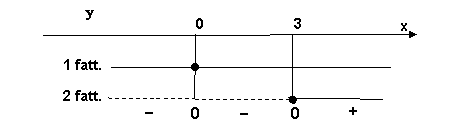
1
fattore: 
cioè 
,
2
fattore: 
cioè 
.
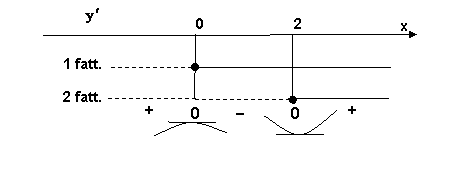
Quindi,
la derivata prima è negativa per 
, pertanto, la funzione data è decrescente per , mentre negli
intervalli dove la derivata prima è positiva, cioè per e per 
, la cubica è crescente. Infine, nei punti dove
la derivata prima è nulla si ha che la funzione data è costante, ossia per 
e per .
7) Massimi, minimi relativi e
flessi a tangente orizzontale
Nell’intorno
del valore 0 la derivata prima presenta la seguente combinazione di segni:
pertanto
è un massimante,
essendo 
la funzione data ha
nel punto un punto di massimo relativo,
mentre nell’intorno del valore 2 la derivata prima presenta la seguente
combinazione di segni:
pertanto
2 è un minimante, essendo 
la funzione data ha
nel punto
un minimo relativo.
8) Concavità e/o convessità
Si
calcola la derivata seconda della funzione, cioè: 
, si pone poi la derivata seconda maggiore o uguale a zero,
cioè: 
, pertanto si ottiene 
. Quindi la funzione data è concava verso l’alto
nell’intervallo dove la derivata seconda è positiva, ossia per 
, mentre è concava verso il basso nell’intervallo dove la
derivata seconda è negativa, cioè per 
, inoltre la derivata
seconda è nulla per 
.
9) Ricerca di ulteriori punti di flesso
a tangente obliqua
Poiché 
e 
(coefficiente angolare
negativo della retta tangente), la funzione data presenta in 
un punto di flesso a tangente
obliqua discendente. Per determinare l’equazione della retta tangente in 
si applica la seguente
equazione: 
dove 
. Pertanto, si ottiene 
cioè 
.
10)
Grafico
