Prof. Mauro
Analisi Classe Quinta Derivata
RAPPORTO INCREMENTALE
Sia 
una funzione reale definita in un
intervallo 
e sia 
un punto del grafico della funzione, con
la condizione che 
sia un valore interno
all’intervallo, cioè 
.
Indicato con h un numero positivo o
negativo in modo che sia verificata la condizione 
, si dice che si è dato alla
variabile x l’incremento h.
Graficamente si ha:
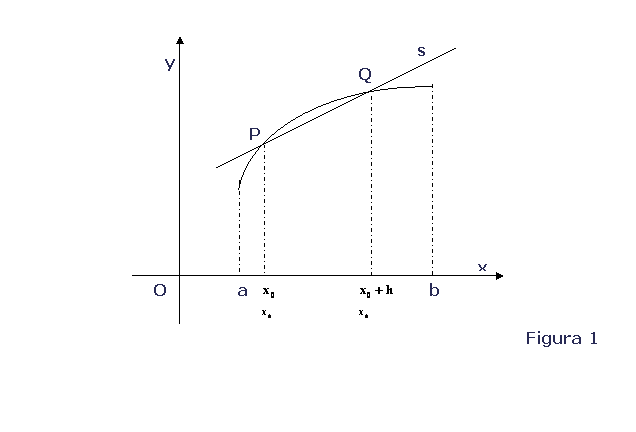
Si dice rapporto incrementale della
funzione relativo al punto di ascissa e all’incremento h la
quantità:
E precisamente
si chiama rapporto incrementale destro se 
,
mentre si dice rapporto incrementale sinistro se 
.
SIGNIFICATO
GEOMETRICO DEL RAPPORTO INCREMENTALE
Ricordando che il coefficiente angolare di una retta è il rapporto tra la differenza delle ordinate e la differenza delle ascisse di due punti qualunque della retta, cioè
,
e prendendo in
considerazione i due punti 
e 
, punti d’intersezione della curva
con la retta secante s (vedi figura 1), risulta che:
.
Ossia:
il rapporto incrementale di una funzione
nell’intorno di un suo punto è il coefficiente angolare della
retta secante passante per il punto dato e per il punto di ascissa
incrementata.
DERIVATA DI UNA
FUNZIONE IN UN SUO PUNTO
Chiamasi derivata della funzione nel suo punto di ascissa il limite, se esiste ed è finito,
del rapporto incrementale della funzione al tendere a zero
dell’incremento h della variabile,
ossia :
.
La derivata
della funzione nel punto di ascissa si suole indicare con una qualunque
delle seguenti notazioni:
,
oppure 
.
La derivata
(prima) della funzione è
quindi definita dalla seguente relazione:
.
Può darsi
che, pur non esistendo il limite per h
che tende a zero del rapporto incrementale, esista e sia finito tuttavia il
limite a desta o il limite a sinistra, questi si chiameranno allora,
rispettivamente, derivata destra e derivata sinistra della funzione in ,
e si rappresenteranno con i simboli 
e 
, si ha quindi, per definizione:
e
.
SIGNIFICATO
GEOMETRICO DELLA DERIVATA
Partendo dal significato geometrico del rapporto incrementale e osservando che al tendere di h a zero, il punto Q tende a P e la retta secante , passante per i punti P e Q , tende a disporsi tangente alla curva nel punto P, si può affermare che:
la derivata di una funzione in un suo punto
è uguale al coefficiente angolare della tangente alla curva in quel
punto.
Graficamente si ha:
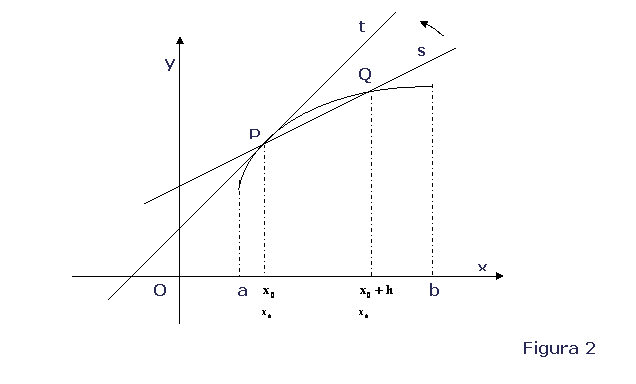
CENNI STORICI
Il concetto di
derivata di una funzione di una variabile è uno dei più importanti
e fecondi della Matematica, ed è quello su cui si basa il calcolo
differenziale. Tracce di questo calcolo si riscontano presso gli antichi
geometri, specialmente in Archimede (matematico e fisico siracusano:
Prof.Mauro
La Barbera