Prof. Mauro
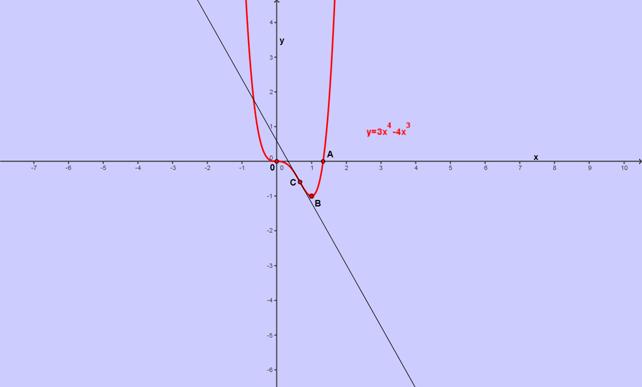
STUDIO COMPLETO DELLA FUNZIONE:
1)
Classificazione e Campo di
esistenza :
Funzione algebrica razionale intera di quarto grado, parabola
quartica, C.E. o dominio della funzione è :
(simbologia insiemistica) , oppure 
(simbologia
topologica).
2) Simmetrie :
Si pone 
allora: 
ossia: 
, quindi la funzione non è simmetrica rispetto
all’asse delle ordinate, cioè non è una funzione pari, perché dal punto di
vista algebrico si ha che 
, inoltre, non è simmetrica rispetto all’origine degli
assi cartesiani, ossia non è una funzione dispari, perché si ottiene che 
.
3)
Studio del segno :
Si pone il secondo membro dell’equazione della funzione maggiore o uguale a zero, cioè:
cioè: 
, pertanto, si può
scrivere:
1 fattore: 
,
2 fattore: 
per 
.
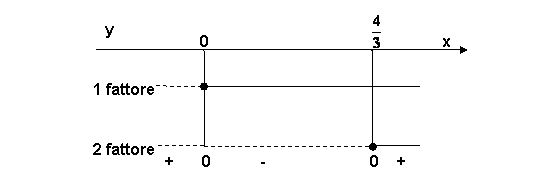
Quindi per 
e per
la funzione è positiva, mentre per 
la funzione è
negativa, infine per 
e per 
la funzione è nulla.
4) Intersezioni con gli assi cartesiani :
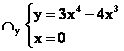
ossia passa per
l’origine degli assi cartesiani.
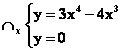
ossia interseca l’asse
delle x, sia nell’origine che nel punto 
.
5) Andamento della funzione agli estremi
dell’intervallo che costituisce il dominio :
e 
.
6) Crescenza e/o
decrescenza :
Si calcola la derivata prima della funzione, cioè: 
, si pone poi la
derivata prima maggiore o uguale a zero, cioè: 
, ossia: 
, pertanto, si ottiene:
1 fattore: 
la disequazione è
sempre verificata nel C.E. , cioè ;
2 fattore: 
per 
.
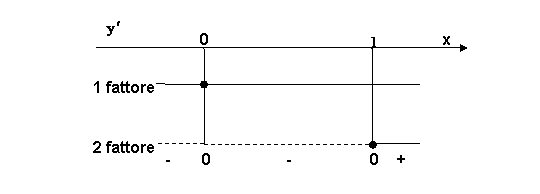
Quindi, la derivata prima della funzione data è negativa per 
e per 
, pertanto, ivi la
funzione è decrescente, mentre la derivata prima della funzione è positiva per 
, allora, ivi la
funzione è crescente. Infine, la
derivata prima è nulla per e per 
, ivi la funzione è
costante. (L’annullarsi della derivata prima è condizione necessaria affinché
esistano punti estremanti, ossia minimanti o massimanti.)
7) Massimi, minimi
relativi e flessi a tangente orizzontale :
La funzione data ha nell’origine degli assi cartesiani un punto di flesso
discendente a tangente orizzontale, mentre ha un minimo relativo nel punto di
ascissa (minimante). Per determinare il valore di minimo si
sostituisce nell’equazione della
funzione, ossia 
. Pertanto, la funzione ha un minimo relativo in 
.
8)
Concavità e/o convessità :
Si calcola la derivata seconda della funzione, cioè: 
.
Si pone poi la derivata seconda maggiore o uguale a zero, cioè: 
, ossia 
, pertanto, si ottiene:
1 fattore: 
;
2 fattore: 
.
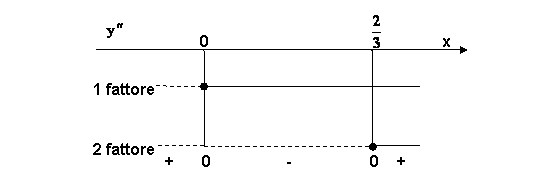
Quindi la derivata seconda della funzione data è positiva per e per 
, pertanto, ivi la funzione
è concava verso l’alto, mentre la derivata seconda della funzione è negativa per 
, ivi la funzione è concava verso il basso,
inoltre, la derivata seconda si annulla per e per 
. (L’annullarsi della
derivata seconda è condizione necessaria affinché esistano punti di flesso.)
9)
Ricerca di ulteriori punti di flesso a tangente obliqua :
La funzione data presenta due punti di inflessione, e precisamente:
, ossia l’origine
degli assi cartesiani, punto di flesso discendente a tangente orizzontale,
(precedentemente trovato) e un punto di flesso a tangente obliqua per . Per determinare l’ordinata del punto di flesso si
sostituisce nell’equazione della
funzione data, cioè 
, pertanto, si ottiene
il punto 
. Infine , per stabilire se è un punto di flesso ascendente o
discendente si osserva che nel valore la derivata prima della funzione risulta
negativa, quindi si può affermare che la tangente obliqua del flesso è
decrescente, quindi il punto è un punto di inflessione discendente.
Osservazioni finali:
Il punto di minimo relativo risulta essere anche
il punto di minimo assoluto.
Per determinare l’equazione della tangente
obliqua del punto di flesso si applica la seguente
formula (equazione della retta passante per un punto): 
dove 
, mentre 
e 
sono le coordinate del
punto di flesso. Pertanto, ha senso scrivere:
quindi
ossia l’equazione della tangente
obliqua del flesso .
La funzione data essendo algebrica razionale intera
non presenta asintoti.
10)
Grafico :
