SIMMETRIE DI UNA FUNZIONE
Un
punto importante nello studio analitico di una funzione è individuare se il relativo
grafico presenta eventuali simmetrie. Infatti se si determina che una curva è simmetrica allora è possibile ridurre
lo studio della funzione del cinquanta per cento. In generale le simmetrie
possono essere del tipo assiale (cioè rispetto ad una retta) o puntuale (cioè
rispetto ad un punto). Se il grafico della curva presenta una simmetria
rispetto all’asse delle ordinate allora la funzione si definisce pari,
algebricamente si verifica la seguente proprietà:
Quando
una funzione è pari è sufficiente studiarla nel semiasse positivo delle
ascisse, per poi ribaltare il grafico nel semiasse negativo, facendo
corrispondere ad ascisse opposte la stessa immagine (ordinata).
Un
esempio di funzione pari è la parabola di equazione
,
graficamente
si ha:
Un altro esempio di funzione pari è la
funzione biquadratica, la cui equazione canonica è
,
ponendo 
,
graficamente si ottiene:
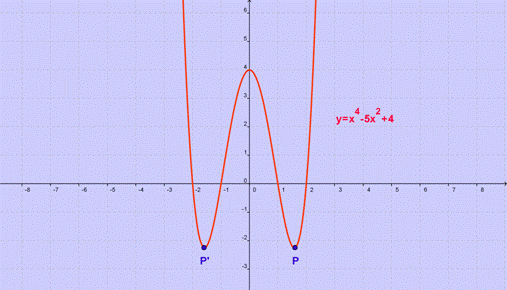
Invece
una funzione si dice dispari quando è simmetrica rispetto all’origine degli
assi cartesiani, ossia algebricamente si verifica la seguente proprietà:
.
Quando
una funzione è dispari è sufficiente studiarla nel semiasse positivo delle
ascisse, per poi ruotare il grafico di un angolo piatto nel semiasse negativo,
facendo corrispondere ad ascisse opposte, immagini opposte.
Un
esempio di funzione dispari è la parabola cubica di equazione
,
graficamente
si ha:
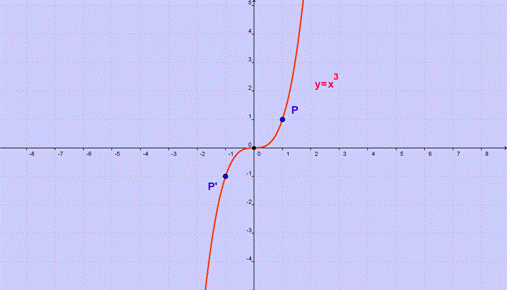
Un altro esempio di funzione dispari è la
funzione iperbole equilatera, la cui equazione canonica è
,
ponendo 
, graficamente si
ottiene:
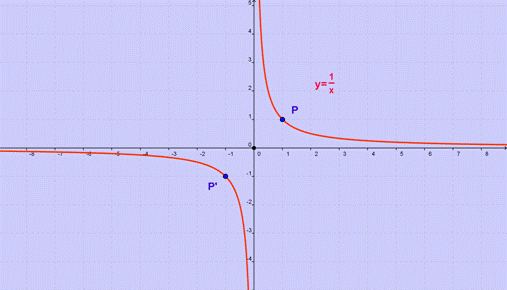
E’ importante osservare che se un grafico
presenta una simmetria assiale rispetto all’asse delle ascisse allora il
disegno della curva non può essere associato all’equazione di una funzione,
perché in corrispondenza di una ascissa del grafico avremmo due ordinate e ciò
andrebbe in contrapposizione con la definizione analitica di funzione, che è
una legge che associa ad un valore della variabile x uno ed un solo valore
della variabile y.
Un esempio di non funzione è la parabola di
equazione
,
graficamente si ha:
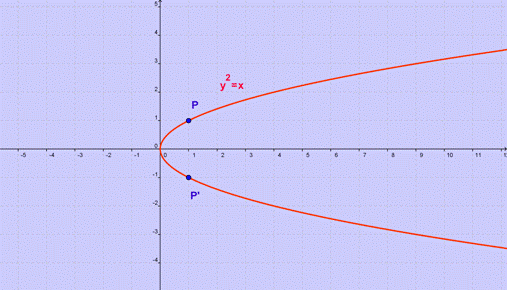
Infine, esistono alcune funzioni, ad
esempio la funzione omografica, la cui equazione canonica è
,
che presenta una simmetria puntuale, ma non è una funzione dispari.
Infatti
l’omografica ha una simmetria rispetto al punto di intersezione tra il
suo asintoto verticale e il suo asintoto orizzontale. Tale punto non coincide
con l’origine degli assi cartesiani perché le sue coordinate sono 
.
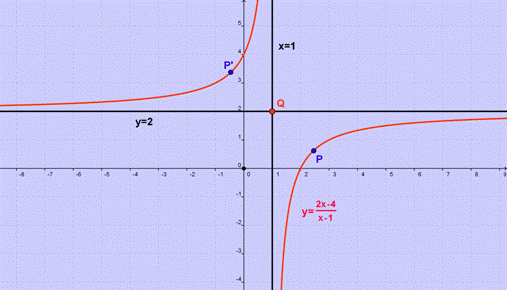
Un esempio è la funzione omografica di
equazione
,
tale funzione è simmetrica rispetto al
punto 
,
come si nota nel seguente grafico:
PROPRIETA’ DELLE FUNZIONI SIMMETRICHE
In generale, la somma (o la differenza) di una
funzione pari e di una dispari non è né pari né dispari,
ad esempio la funzione di equazione
.
La somma di due funzioni pari è una
funzione pari.
La somma di due funzioni dispari è a sua
volta dispari.
Il prodotto ( o il rapporto) di una
funzione pari per una costante è pure pari.
Il prodotto di una funzione dispari per una
costante è pure dispari.
Il prodotto di due funzioni pari è una
funzione pari.
Il prodotto di due funzioni dispari è una
funzione pari.
Il prodotto di una funzione pari e di una
funzione dispari è una funzione dispari.
La derivata di una funzione pari è dispari.
La derivata di una funzione dispari è pari.
Geometria analitica argomento correlato: simmetrie tra punti del piano