STUDIO COMPLETO DELLA FUNZIONE OMOGRAFICA:
Esempio:
1) Classificazione e C.E.:
Funzione algebrica razionale fratta di secondo grado (omografica),
C.E.: 
.
2) Simmetrie :
Non è simmetrica sia rispetto all’asse y sia rispetto all’origine.
3) Studio del segno :
Si pone: 
ossia:
La funzione è positiva per 
, è negativa per 
, è nulla per 
, non esiste per 
.
4) Intersezione con gli assi cartesiani :
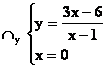
5) Asintoti
:
La funzione ha due asintoti: uno verticale ed uno orizzontale, infatti,sapendo che
e 
allora è l’equazione
dell’asintoto verticale.
Inoltre,
,
forma d’indecisione, quindi per poter calcolare il limite si può applicare il Teorema di De L’Hôpital, pertanto, si ottiene:
,
analogamente si ha per 
, allora 
è l’equazione
dell’asintoto orizzontale.
6) Crescenza o decrescenza :
Calcolando la derivata prima si ha:
,
studiando il segno della derivata prima si ottiene:
,
,
pertanto, essendo la derivata prima sempre positiva nel suo dominio, la funzione data è sempre crescente, quindi non possono esistere massimi, minimi relativi e punti di flesso a tangente orizzontale.
7) Concavità e convessità :
Calcolando la derivata seconda si ha:
,
studiando il segno della derivata seconda della funzione si ottiene:
,
,
pertanto, per 
la derivata
seconda è negativa, quindi la funzione data è convessa, mentre per 
la derivata
seconda è positiva quindi la funzione data è concava, pertanto, non possono
esistere punti di flesso a tangente obliqua.
8) Grafico :
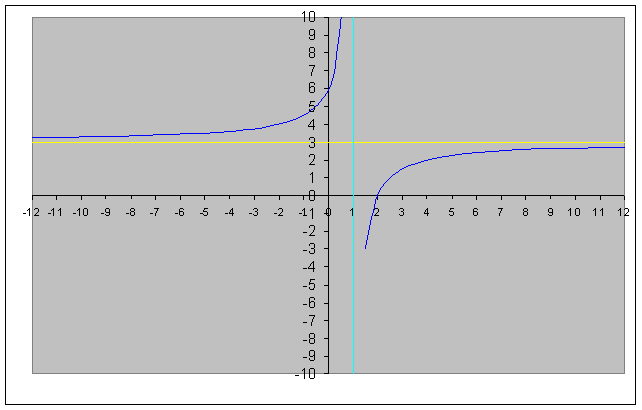
Osservazioni:
Si
chiama funzione omografica la funzione
con a, b, c (distinto da zero) e d coefficienti reali.
In
una funzione omografica per determinare sia l’asintoto verticale sia l’asintoto
orizzontale si possono utilizzare le seguenti formule:
ASINTOTO VERTICALE 
,
ASINTOTO ORIZZONTALE 
.
La
funzione omografica è simmetrica nel punto d’intersezione dei suoi asintoti,
inoltre, mediante la traslazione che porta il punto 
nel punto 
essa assume la
forma dell’iperbole equilatera avente come nuovo sistema di assi cartesiani i
sui asintoti.
Teorema
di De L’Hôpital :
Data una funzione del tipo: 
, se si
verifica che 
allora sussiste
la seguente regola: 
.