Prof. Mauro La Barbera

Home page

ESERCIZIO SVOLTO

Calcolare il punto d’intersezione A tra la retta r e la retta s, dove r è la tangente alla parabola di equazione nel punto di tangenza Ped s è la tangente alla circonferenza C di equazione nel punto di tangenza Q.

Per trovare la retta tangente r alla parabola nel punto di tangenza P si può applicare la seguente regola dello sdoppiamento:

sapendo che

sostituendo si ha

Cioè la retta r ha equazione

.

Analogamente per trovare la retta tangente s alla circonferenza nel punto di tangenza Q si può applicare la seguente regola dello sdoppiamento:

sapendo che

sostituendo si ha

Cioè la retta s ha equazione

Per determinare le coordinate del punto d’intersezione A si deve risolvere il seguente sistema:

Applicando il metodo del confronto si ottiene

Quindi

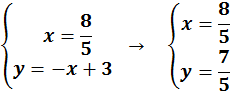
Pertanto si sono trovate le coordinate del punto d’intersezione tra le due rette tangenti, cioè

.

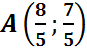Graficamente si ottiene: