Prof. Mauro
TEORIA DELL’ASINTOTO ORIZZONTALE
NELLE FUNZIONI ALGEBRICHE RAZIONALI FRATTE
Data una funzione algebrica razionale
fratta del tipo
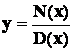
nella ricerca dell’asintoto
orizzontale si possono verificare i seguenti casi:
1.
Se il numeratore ed il denominatore hanno lo stesso grado
allora esiste un asintoto orizzontale di equazione 
, dove a è il rapporto dei
coefficienti della variabile x di grado massimo.
ESEMPIO:
La funzione
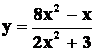
ha l’asintoto orizzontale di
equazione
.
2.
Se il grado del denominatore è maggiore di
quello del numeratore allora esiste un asintoto orizzontale di equazione 
, ossia la curva
è asintotica all’asse delle ascisse.
ESEMPIO:
La funzione
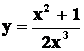
ha l’asintoto orizzontale di
equazione
.
3.
Se il grado del numeratore è maggiore di quello
del denominatore allora la funzione non ammette asintoto orizzontale.
ESEMPIO:
La funzione
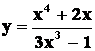
non ammette asintoto orizzontale.
TEORIA DELL’ASINTOTO OBLIQUO
NELLE FUNZIONI ALGEBRICHE RAZIONALI FRATTE
Data una funzione algebrica razionale fratta del tipo
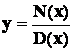
l’asintoto obliquo esiste soltanto se si
verifica la seguente condizione:
Se il grado del numeratore è
maggiore di una unità rispetto a quello del denominatore allora esiste
l’asintoto obliquo di equazione 
, dove m ed n sono rispettivamente il
coefficiente angolare e l’intercetta
della retta.
Per determinare m si applica la seguente formula:
,
mentre per determinare n si applica la seguente formula:
.
ESEMPIO:
Data la funzione di equazione
si ha:
,
.
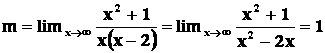Quindi la funzione data è asintotica alla retta
obliqua di equazione:
.