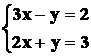Prof.
Mauro
ESERCIZIO SVOLTO SISTEMA
LINEARE
METODO DI SOSTITUZIONE
Per risolvere il sistema proposto a due equazioni in due incognite si
ricava il valore di una variabile in una delle due equazioni, ad esempio:
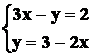
Si sostituisce il valore di y della
seconda equazione nella prima equazione, ossia:
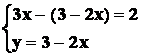
Risolvendo la prima equazione si ottiene:
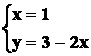
Sostituendo il valore trovato della 
nella seconda
equazione si ha:
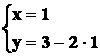
Quindi il sistema dato ammette per soluzioni la seguente coppia di
valori:
.
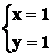METODO DI
RIDUZIONE
Addizionando membro a membro, si ha:
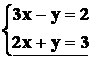
ossia
Moltiplicando la prima equazione per
due e la seconda per tre, ha senso scrivere:
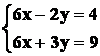
Sottraendo membro a membro, si ha:
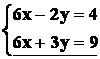
ossia 
.
METODO DI
PARAGONE
Si ricavano i valori della variabile nelle due equazioni,
cioè:
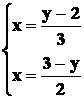
Dall’uguaglianza dei primi membri segue
l’uguaglianza dei seguenti membri, ossia:
Risolvendo l’equazione in y si ottiene: y = 1
Si ricavano i valori della variabile y nelle
due equazioni, cioè:
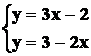
Dall’uguaglianza dei primi membri segue
l’uguaglianza dei seguenti membri, ossia:
Risolvendo l’equazione in si ottiene: .
METODO DI CRAMER
Per risolvere il sistema dato bisogna ricordare che la sua forma
canonica è:
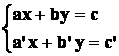
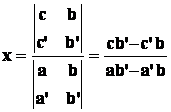
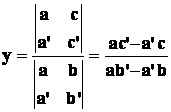
Per determinare le soluzioni si applicano le seguenti formule:
Pertanto, sostituendo i valori dei coefficienti a, b e
c nelle due formule suddette si ha:
.
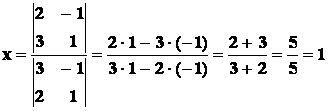
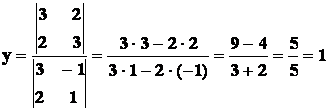