Prof.
ESERCIZI SVOLTI SULLA PARABOLA
1) Determinare l'equazione della parabola
passante per i punti 
,
e 
.
Tracciare, inoltre, il grafico della curva.
Ricordando che le coordinate
di un punto della parabola sono le soluzioni dell’equazione associata alla
curva, per determinare l’equazione della parabola bisogna risolvere il sistema
formato da tre equazioni in tre incognite. Le equazioni del sistema sono
ottenute sostituendo, rispettivamente, nell’equazione canonica della parabola 
le coordinate dei punti A, B e C.
Ossia:
Ordinando il sistema si ottiene:
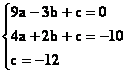
Applicando, ad esempio, il metodo di
sostituzione si ottengono le seguenti soluzioni:
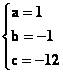
Ossia l’equazione della parabola è
.
Graficamente, si ha:
2) Determinare l'equazione della parabola avente il vertice in 
e passante per 
. Tracciare, inoltre, il grafico della curva.
Primo metodo
Sapendo che
l’ascissa del vertice è data dalla seguente formula: 
,
si impone l’uguaglianza con il valore corrispondente dato, cioè:
, ossia 
.
Inoltre, si
impone la condizione di appartenenza del punto V alla curva (
),
ossia le coordinate del punto V sono le soluzioni dell’equazione della
parabola, cioè:
. ossia 
.
Infine, si
impone la condizione di appartenenza del punto P alla curva (
),
ossia le coordinate del punto P sono le soluzioni dell’equazione della
parabola, cioè:
ossia 
Pertanto, si mettono a sistema le tre
equazioni ottenute:
Applicando il
metodo di sostituzione e sapendo che e si ottiene:
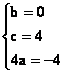, ossia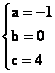 
Ossia l’equazione della parabola è
.
Secondo
metodo
Si può arrivare alla stessa conclusione, se
si applica la seguente formula:
dove 
e 
indicano,
rispettivamente, l’ascissa e l’ordinata del vertice.
Per applicare la formula suddetta, conviene procedere nel seguente
modo:
1°passaggio: sostituire nella formula le coordinate del vertice,
ossia:
,
2°passaggio: sostituire nella relazione precedente le coordinate
del punto P, ossia:
,
da cui si deduce
cioè 
3°passaggio: sostituire il valore di A nella relazione del
1°passaggio, ossia:
,
ossia
cioè l’equazione della parabola è
.
Graficamente,
si ha:
