Nel linguaggio comune la parola insieme è sinonimo di raccolta, aggregato, collezione, classe ed ecc. Invece, in Matematica non esiste una definizione d’insieme. Il concetto d’insieme deve essere considerato un concetto primitivo (o ente fondamentale), ossia un ente (una cosa) di cui si intuisce il significato ma non si può definire. Pertanto, non si può definire il concetto d’insieme, ma si può sempre stabilire se un dato oggetto appartiene o no ad un insieme. Si può stabilire, senza possibilità di equivoci, che un dato oggetto appartiene ad un insieme se verifica una determinata proprietà che caratterizza la formazione dell’insieme. Ad esempio, gli oggetti a, e, i, o, u fanno parte di uno stesso insieme, cioè l’insieme delle vocali dell’alfabeto italiano, quindi l’essere una vocale è la proprietà che costituisce l’insieme, cioè è la proprietà caratterizzante dell’insieme. Se si considera la lettera m si può affermare che non appartiene all’insieme considerato, perché ovviamente non è una vocale, ma una consonante. Gli oggetti di un insieme si chiamano elementi e si indicano con le lettere minuscole dell’alfabeto, mentre gli insiemi si denotano con lettere maiuscole. Per indicare che un dato elemento appartiene ad un insieme, cioè verifica la proprietà caratterizzante dell’insieme, si usa il simbolo , mentre si usa il simbolo  per dire che l’elemento non appartiene all’insieme o che non verifica la legge di formazione dell’insieme.

Se si indica con V  l’insieme delle vocali dell’alfabeto, allora ha senso scrivere:

 

  ossia a appartiene all’insieme V  ,    ossia m non appartiene all’insieme V,

 

Rappresentazione di un insieme

v    Rappresentazione grafica (o di Eulero – Venn)

Per rappresentare graficamente gli insiemi, di solito, si utilizzano i diagrammi di Eulero – Venn, nei quali gli elementi degli insiemi sono racchiusi dentro linee chiuse (di solito ovali), inoltre, gli oggetti si segnano con un punto.

Ad esempio, l’insieme V si rappresenta nel seguente modo:

 

 

Invece, se si vuole evidenziare che un elemento non appartiene all’insieme, lo si indica con un punto esterno alla linea chiusa, ad esempio, nel disegno seguente si mette in luce che la lettera m non appartiene all’insieme V:                                                                                                                                                                                     .m

 

v    Rappresentazione estensiva (o tabulare o per elencazione o analitica)

Nella rappresentazione estensiva gli elementi vengono elencati, racchiusi fra parentesi graffe e separati da virgole (o da punti e virgole). Inoltre, gli elementi non devono essere ripetuti e non ha importanza l’ordine con cui sono scritti, (anche se l’ordine a volte può essere comodo nell’individuare gli oggetti). Ad esempio, l’insieme V si rappresenta nel seguente modo:

 

Se si vuole rappresentare l’insieme F delle lettere della parola sasso dal punto di vista tabulare, si ha la seguente scrittura:

 

Indicando con C l’insieme di tutti i numeri naturali maggiori o uguali a 2 e minori di 7, la rappresentazione estensiva è data dalla seguente forma:

 

 

v    Rappresentazione intensiva (o sintetica)

Nella rappresentazione intensiva di un insieme si mette in evidenza la proprietà che  caratterizza in modo oggettivo ed univoco ogni suo elemento, cioè si scrive dentro le parentesi graffe un generico elemento, di solito denotato con x, seguito dalla legge di formazione, alla quale soddisfano tutti gli elementi appartenenti all’insieme.

Ad esempio, l’insieme V si rappresenta sinteticamente nel seguente modo:

 

/ x

 

L’insieme C , precedentemente denominato, si rappresenta dal punto di vista intensivo nel seguente modo:

 

Insieme vuoto

Un insieme privo di elementi si chiama insieme vuoto, ossia  è un insieme per il quale non si riesce a determinare nessuno oggetto che verifica la proprietà di formazione dell’insieme stesso. Ad esempio, un insieme vuoto è l’insieme di tutti i numeri quadrati maggiori di 4 e minori o uguali a 8. Si suole indicare l’insieme vuoto utilizzando indifferentemente i simboli: Ø oppure .

 

Insiemi uguali

Si dicono uguali due insiemi che risultano costituiti dagli stessi elementi. Ad esempio, consideriamo l’insieme M dei numeri naturali dispari minori o uguali a 7 e maggiori o uguali a 3, e l’insieme N dei numeri naturali primi maggiori di 2 e minori di 11.  Rappresentando i due insiemi suddetti dal punto di vista tabulare si ottiene:

  e 

 

I due insiemi, evidentemente, hanno gli stessi elementi, quindi sono uguali, cioè . Per denotare, invece, che due insiemi sono disuguali si usa il simbolo: . Ad esempio, l’insieme A delle lettere della parola vaso e l’insieme B delle lettere della parola rosa, sono insiemi disuguali, perché costituiti da elementi distinti, infatti, rappresentandoli dal punto di vista grafico si ottiene:

 

 

 

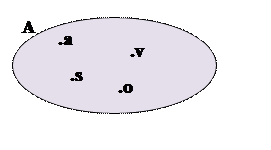
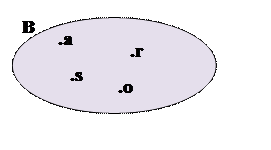
Sottoinsieme

Dati due insiemi E ed F, se tutti gli elementi dell’insieme F appartengono all’insieme E, ma esistono elementi di E che non appartengono ad F si dice che l’insieme F è sottoinsieme (proprio) dell’insieme E. In simboli si scrive: . Ad esempio, siano E l’insieme delle lettere della parola cosa, ed F l’insieme delle lettere della parola casa. Rappresentando i due insiemi dal punto di vista estensivo si ottiene:

      

E’ evidente che tutti gli elementi dell’insieme F sono anche elementi dell’insieme E, mentre in E esiste un elemento che non appartiene ad F, ossia  . I due insiemi suddetti si possono rappresentare graficamente nel seguente modo:

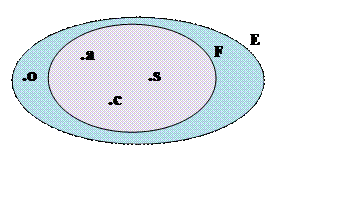
Per ogni insieme, non vuoto, si è stabilito che esistono due sottoinsiemi banali (o impropri), ossia l’insieme stesso e l’insieme vuoto. Per scrivere che un insieme è contenuto impropriamente in se stesso, si usa la seguente simbologia:  .

 

La relazione di inclusione impropria (o in senso largo) gode delle seguenti tre proprietà:

 

v   Riflessiva: , ossia   A è incluso impropriamente in se stesso.

v   Antisimmetrica:  se A Í B  e B Í A allora A = B , ossia se A è incluso impropriamente in B e viceversa, allora A e B sono lo stesso insieme.

v   Transitiva:   , ossia se A è incluso impropriamente in B e B è incluso impropriamente in C allora A è incluso impropriamente in C.

 

Insieme finito ed insieme infinito

Un insieme si dice finito se è possibile elencare tutti i suoi elementi, in caso contrario si dice infinito, è ovvio che l’insieme vuoto, ossia l’insieme privo di elementi, è considerato un insieme finito. Ad esempio, l’insieme di tutti i divisori del numero 10 è un insieme finito, mentre l’insieme di tutti i multipli di 10 è un insieme infinito.

 

Insieme delle parti

Si definisce insieme delle parti di un insieme A (non vuoto), l’insieme che ha per elementi tutti i sottoinsiemi propri ed impropri di A. L’insieme delle parti di A si può indicare con il simbolo .

Ad esempio, si vuole determinare l’insieme delle parti dell’insieme A costituito da tutte le lettere della parola dado.

 

Essendo  , i suoi sottoinsiemi propri sono:

Mentre i sottoinsiemi impropri (o banali) di A sono:  

 

Pertanto, l’insieme delle parti di A è dato:

 

.

 

Secondo esempio:

si vuole trovare l’insieme delle parti dell’insieme   .

 

I sottoinsiemi propri di B sono 

 

I sottoinsiemi banali di B sono 

 

Pertanto, l’insieme delle parti di B è dato:

 

.

 

Dagli esempi precedenti, si  osserva che il numero degli elementi di A è 3 , mentre gli elementi di    sono 8 ( 2³ ) , il numero degli elementi di B è 2 , mentre gli elementi di   sono 4  ( 2² ) , quindi è facile dedurre che se in generale il numero degli elementi di un insieme è n il numero degli elementi dell’insieme delle parti è costituito da 2ⁿ .

Torna su