LA FUNZIONE
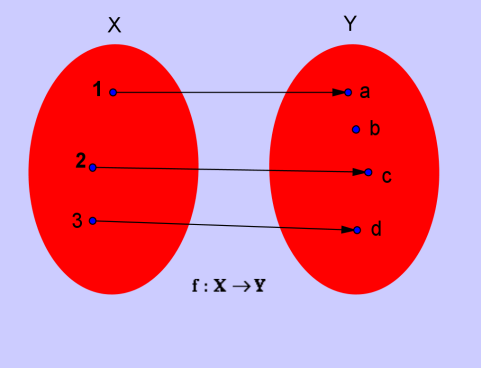
Dati due insiemi non vuoti si dice funzione
una relazione (o legge) f tale che per ogni
elemento del primo insieme esiste uno ed
un solo elemento del secondo insieme.
Il primo insieme X è il dominio della funzione,
l'insieme Y in cui si trovano i valori associati al primo
insieme si chiama codominio e i suoi elementi
si chiamano immagini e si indicano con f(x).
Gli elementi di X si chiamano controimmagini e si indicano con f-1(y).
ESEMPI DI NON FUNZIONE
LA FUNZIONE INIETTIVA
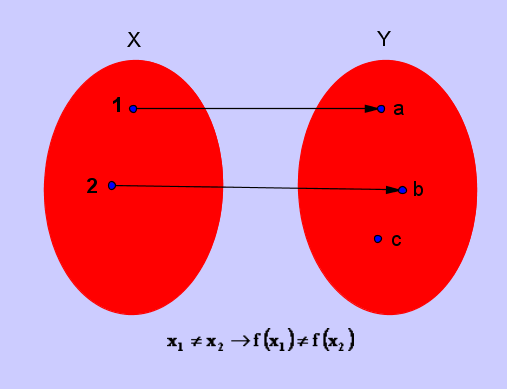
Una funzione iniettiva è una funzione che associa
elementi distinti del primo insieme in elementi
distinti del secondo insieme.
Una funzione è iniettiva quando tracciata
una qualunque retta orizzontale essa
interseca il grafico della curva in un solo punto.
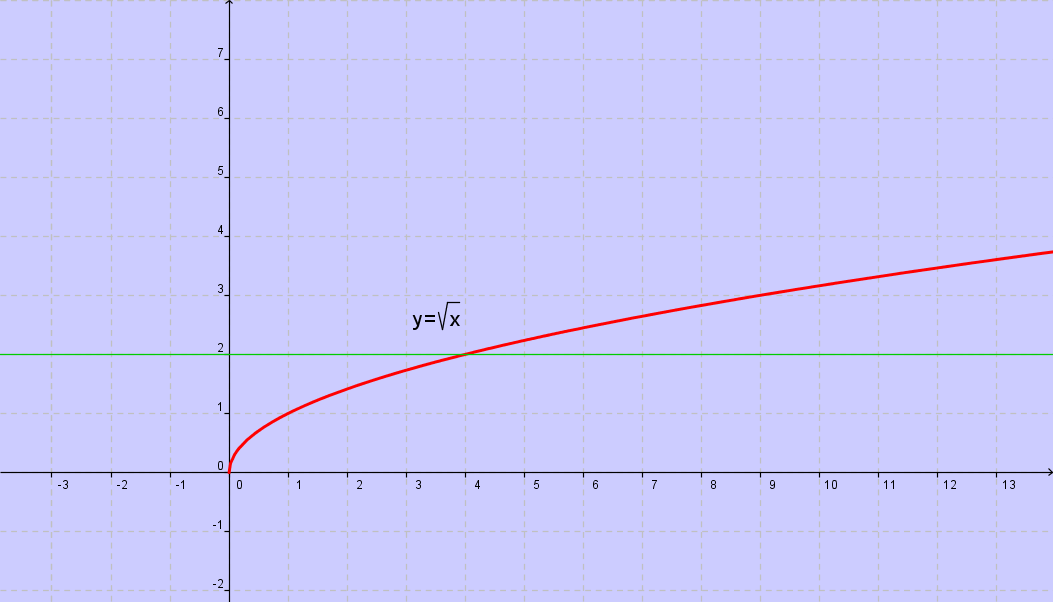
ESEMPIO DI FUNZIONE INIETTIVA RAMO DI PARABOLA
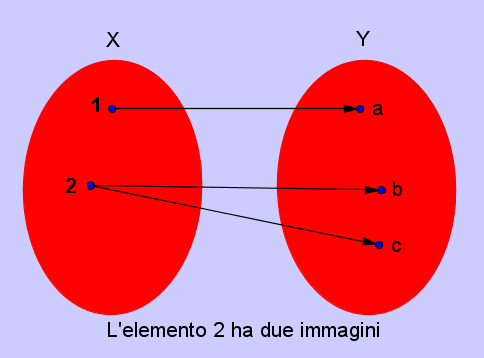
ESEMPIO DI FUNZIONE NON INIETIVA
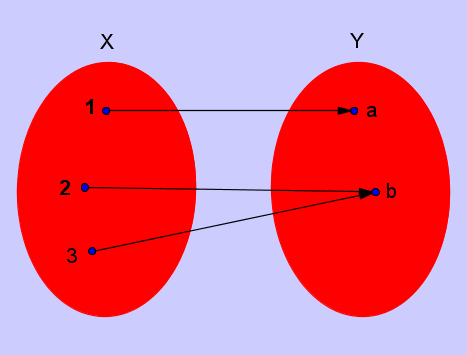
Gli elementi 2 e 3 vengono mandati entrambi
nell'elemento b, ossia
f(2) = b e f(3) = b
PARABOLA
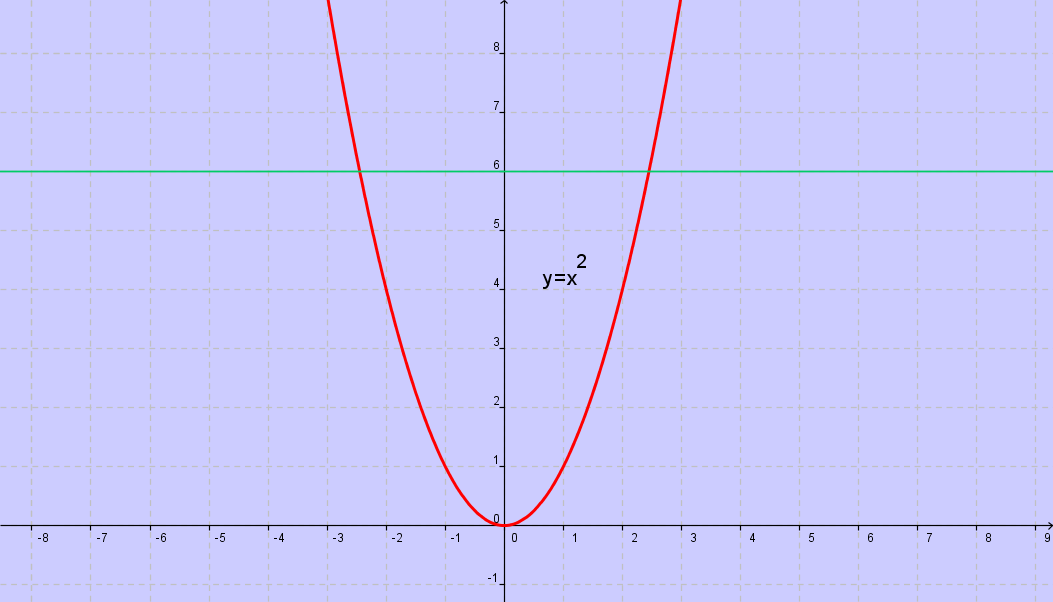
LA FUNZIONE SURIETTIVA

Una funzione si dice suriettiva quando ogni
elemento del secondo insieme è immagine
di almeno un elemento del primo insieme.
In tal caso si ha che il codominio coincide
con il secondo insieme, ossia con l'insieme immagine.
Una funzione è suriettiva quando tracciata
una qualunque retta orizzontale essa
interseca sempre il grafico della curva.
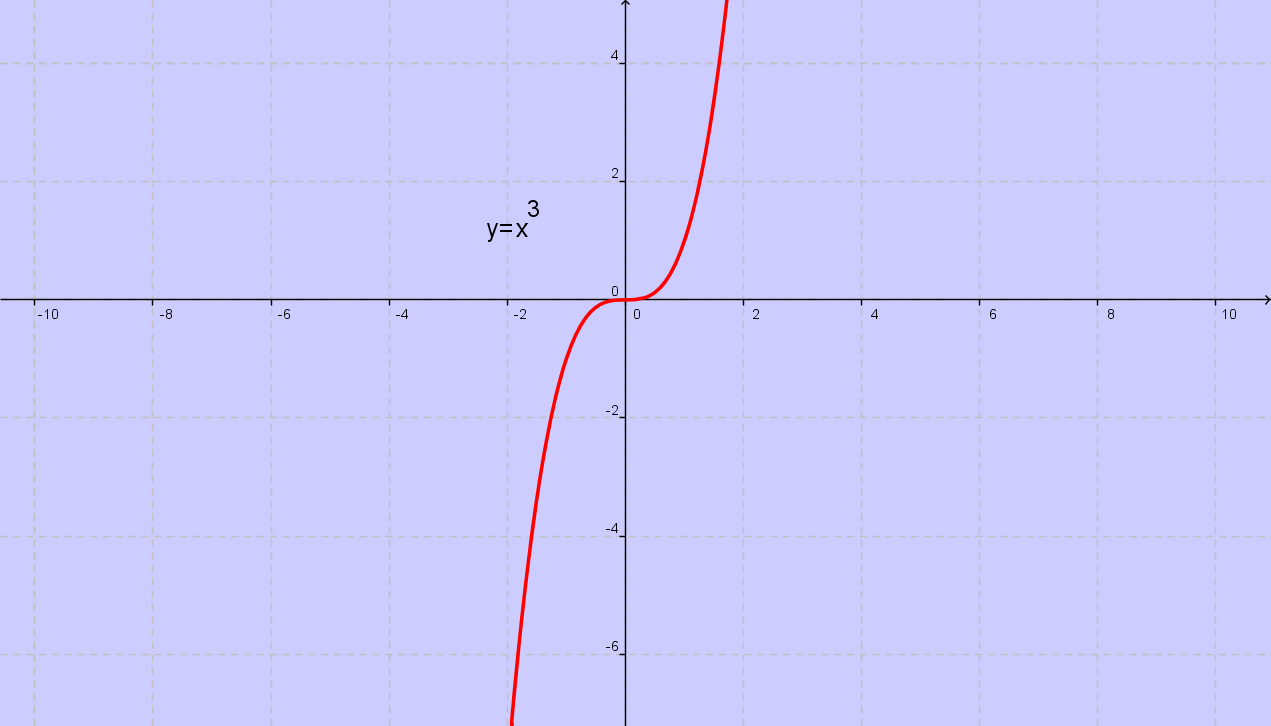
ESEMPIO DI FUNZIONE SURIETTIVA PARABOLA CUBICA SPURIA
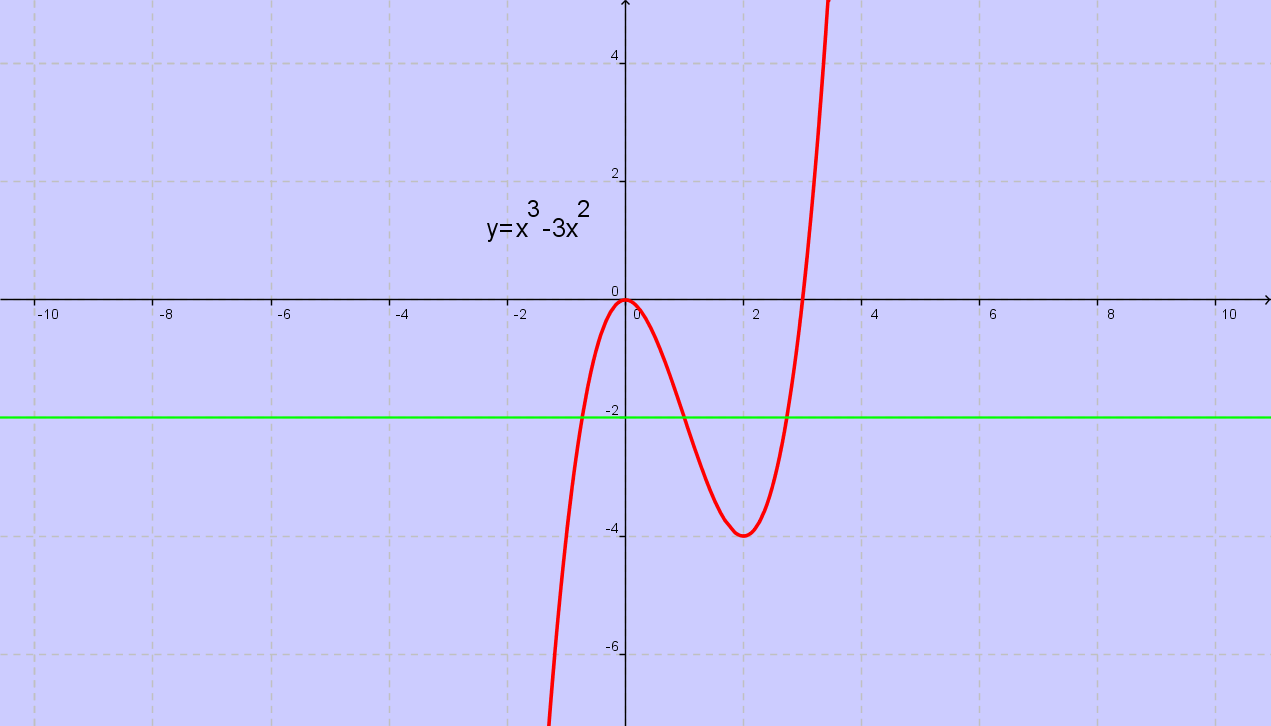
(SURIETTIVA, MA NON INIETTIVA)
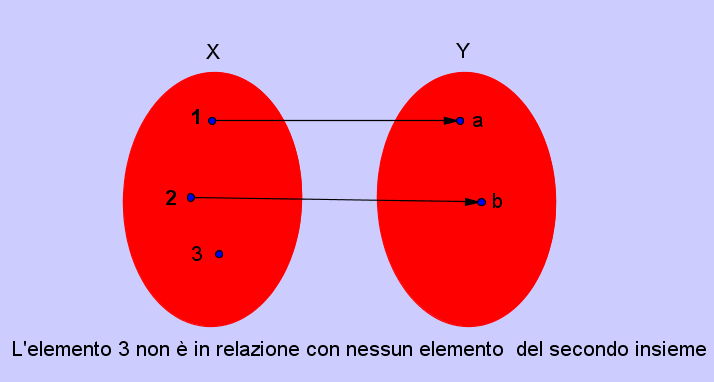
ESEMPIO DI FUNZIONE NON SURIETTIVA
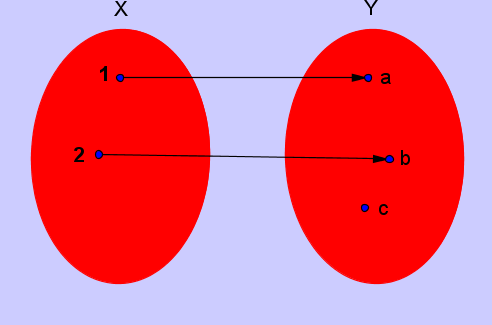
L'elemento c non è immagine di nessun
elemento del primo insieme.
PARABOLA
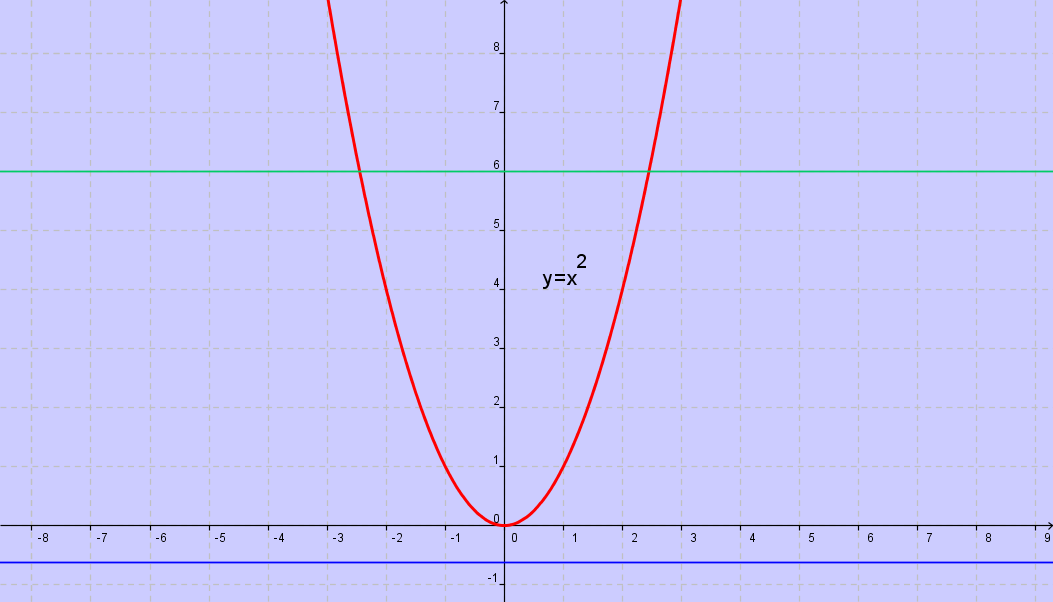
FUNZIONE NON SURIETTIVA (E NON INIETTIVA)
LA FUNZIONE BIIETTIVA
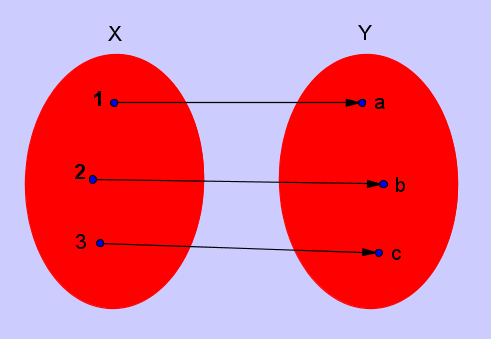
Una funzione si dice biunivoca o biiettiva
quando ad ogni elemento del primo
insieme corrisponde uno ed un solo elemento
del secondo insieme e viceversa.
Una funzione è biiettiva se e solo se è
contemporaneamente iniettiva e suriettiva.
Una funzione biiettiva è invertibile, cioè si ha
l'esistenza della funzione inversa.
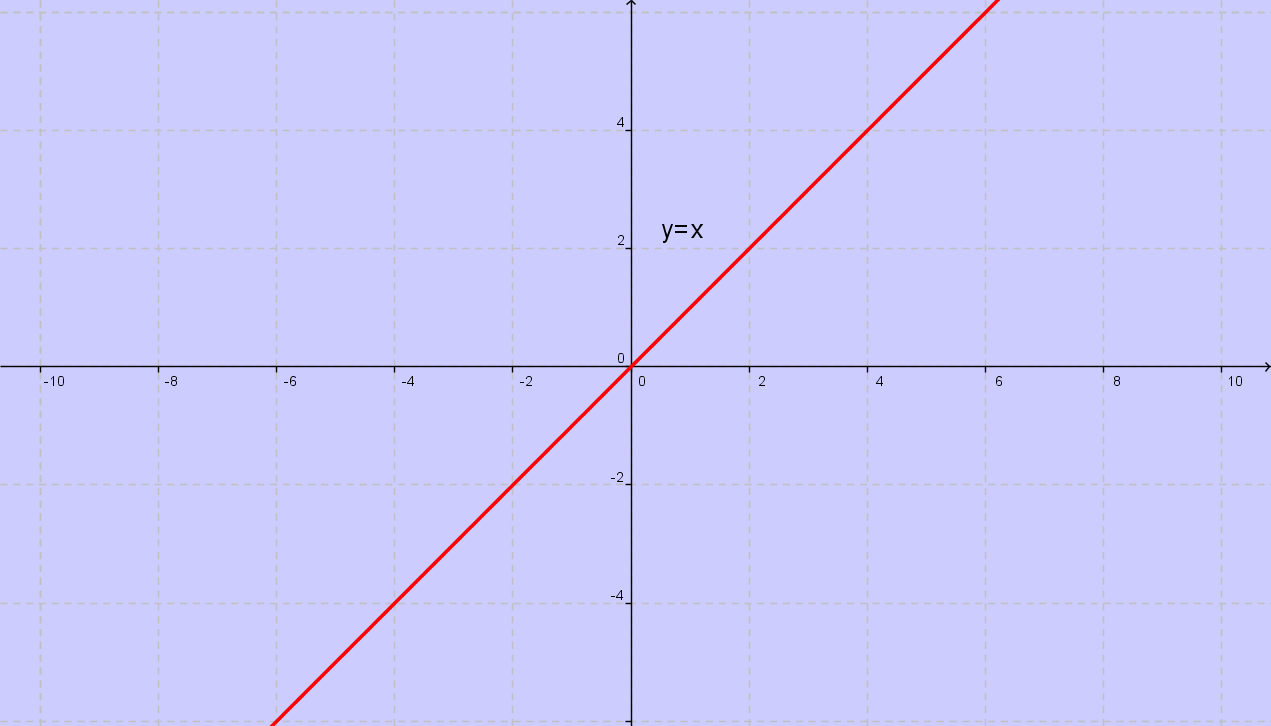
I grafici di due funzioni inverse sono simmetrici
rispetto alla bisettrice del primo e del terzo quadrante.
ESEMPIO DI FUNZIONE BIIETTIVA PARABOLA CUBICA MONOMIA
ESEMPIO DI FUNZIONE BIIETTIVA BISETTRICE DEL PRIMO E TERZO QUADRANTE