,
,
e
,
determinare i punti medi del lati, la misura delle diagonali e le loro
equazioni, il baricentro, il perimetro e l’area della figura. Inoltre,
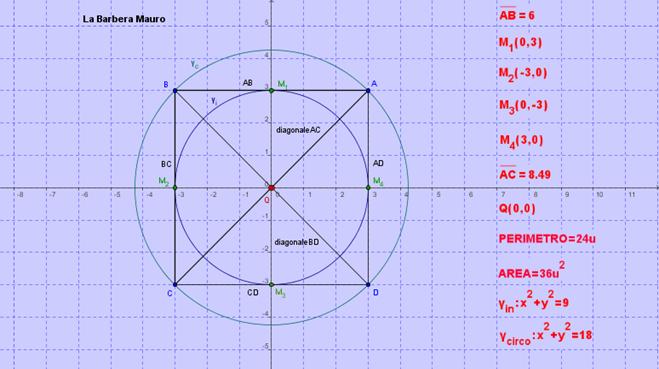
l’equazione sia della circonferenza inscritta che circoscritta al quadrato.QUADRATO
Problema svolto
Dato il quadrato ABCD avente per vertici
,
,
e
,
determinare i punti medi del lati, la misura delle diagonali e le loro
equazioni, il baricentro, il perimetro e l’area della figura. Inoltre,
l’equazione sia della circonferenza inscritta che circoscritta al quadrato.
Il punto medio di un lato
del quadrato è il punto che divide il lato in due parti congruenti. Indicando
con 
il
punto medio del lato AB, per determinare le coordinate del punto si applica la
seguente formula:
.
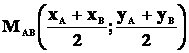Quindi, sostituendo i valori delle coordinate, si ottiene:
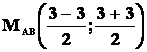cioè 
.
Analogamente, si trovano gli altri punti medi, ossia:
,
e
.
Il quadrato ha due diagonali congruenti ( la diagonale è il segmento che congiunge due vertici opposti), le quali sono tra loro ortogonali. Per trovare la misura, ad esempio, della diagonale AC, si applica la seguente formula:
.
Quindi, sostituendo i valori delle coordinate, si ottiene:
.
Ovviamente anche la
diagonale 
.
Per determinare l’equazione della diagonale AC, si applica la seguente formula:
.
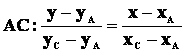Quindi, sostituendo i valori delle coordinate, si ottiene:
.
Si osserva dal risultato suddetto che l’equazione della diagonale AC è l’equazione della bisettrice del primo e terzo quadrante.
Analogamente, si trova l’equazione dell’altra diagonale, ossia:
,
cioè l’equazione della bisettrice del secondo e quarto quadrante.
Il baricentro G del quadrato ABCD è il punto d’intersezione delle sue diagonali. Si applica la seguente formula:
.
Quindi, sostituendo i valori delle coordinate, si ottiene:
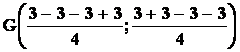cioè 
,
ossia il baricentro coincide con l’origine degli assi cartesiani.
Il quadrato è un quadrilatero che ha tutti i quattro lati (e gli angoli) congruenti, pertanto, per determinare il perimetro, basta calcolare la misura di un lato e moltiplicarla per quattro. Per trovare la misura, ad esempio, del lato AB, osservando che i punti A e B hanno la stessa ordinata, si applica la seguente formula:
.
Pertanto, si ottiene:
.
Pertanto, il perimetro del quadrato ABCD è:
.
L’area del quadrato è data dalla formula lato per lato, quindi ha senso scrivere:
Osservazione
Ogni diagonale del quadrato divide la figura in due triangoli congruenti, pertanto, un altro metodo per determinare l’area del quadrato è quello di calcolare il doppio dell’area di uno dei triangoli. Ad esempio, si può calcolare l’area del triangolo ABC, quindi, è possibile applicare la seguente formula:
.
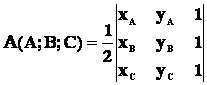Sostituendo i valori delle coordinate dei vertici del triangolo ABC si ottiene:
.
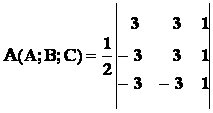Per calcolare il determinate si può procedere nel seguente modo:
=
.
Pertanto, l’area del triangolo ABC è:
.
Mentre l’area della figura è:
Per determinare
l’equazione della circonferenza inscritta al quadrato, si osserva che ha il
centro coincidente con il baricentro della figura e il diametro uguale al lato
del quadrato, quindi indicando con 
il
raggio della circonferenza inscritta, ha senso scrivere:
Pertanto, si applica la seguente formula:
.
Osservando che
,
si ottiene:
,
cioè
.
Per determinare
l’equazione della circonferenza circoscritta al quadrato, si osserva che ha il
centro coincidente con il baricentro della figura e il diametro uguale alla
diagonale del quadrato, quindi indicando con
il
raggio della circonferenza circoscritta, ha senso scrivere:
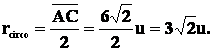
Osservando in
questo caso che 
,
si ottiene:
,
cioè
.
Graficamente:
